研究プロジェクト
初めて宇宙プラズマに接する方へ
地球は、自ら持っている地球磁場により、太陽風磁場の領域と境界面を形成しています。この境界面を(地球)磁気圏境界面[Magnetopause]と言います。 地球磁気圏は大雑把に言うと、太陽風から地球を守るバリアの役割をし、磁気圏に沿ってその流れを変えてくれています。 でも、厳密に言うと、地球磁気圏と太陽風領域本体は直接、隣あってはいなくて、それらの間を埋めるように、太陽風領域から磁気圏領域に遷移する空間が存在しています。それをマグネトシース[Magnetosheath]と言います。マグネトシースは基本的には太陽風領域なのですが、非常に乱れが生じているために、内側に行けば行くほど地球磁気圏の影響が出てきます。
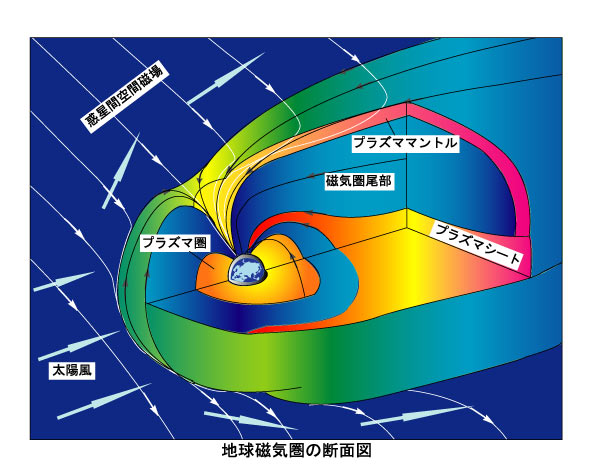
このようなことから、磁気境界面付近は、プラズマにとっては太陽風の影響、磁気圏内部の影響の効果がごちゃ混ぜになっているので、この領域をひっくるめて、磁気圏境界層[Mangetospheric boundary layer]と呼んでいます。要するに、磁場での分類と、プラズマで見た分類が多少異なっているのです。ちなみに、磁気圏境界層の厚さは、千km~数万 kmと言われています。 とにかく、磁気圏境界層は「太陽風と地球磁場が接している周辺」に出来ています。一つは、地球の極域の上空にあります。ちょうど棒磁石の先っぽ付近と考えてもらえばよいです。そこの磁場配置は、ロウトの形をしているのが分かると思います。この領域は太陽風、具体的にはマグネトシースのプラズマがもっとも地球に入り込める様相を呈してます。このロウト領域は(形状からもわかるように)、磁気圏内部のプラズマと言うよりもむしろ、マグネトシースのプラズマ環境に似ています。実際、観測によるとプラズマの密度はマグネトシース領域と同程度で、温度も多少は高いながらもまぁ合っていて、プラズマの速さは乱れていました。
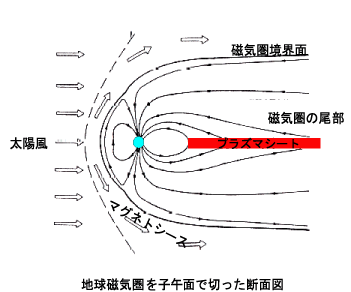
注釈:地球磁気圏を子午面で切った図。水色は地球。マグネトシースは、地球磁気圏境界面と、太陽風本体の間にあり、マグネトシース内で太陽風の流れが急激に曲げられることから、非常に乱れた速度状態が実現される。
2つ目は磁気圏の一番前面から、磁気圏の横腹あたりに存在する、低緯度境界層[Low latitude boundary layer]です。低緯度境界層は前面で厚さ数百km、横腹で1万kmに及びます。低緯度境界層内部のプラズマの流れは、その外側に流れているマグネトシースの流れとかなり似た様子です。実はこの低緯度境界層の理解(例えば、この内部の磁場はどのような形状をしているのか、また、地球磁場と太陽風磁場は本当にリコネクションを起こしているのかなどなど)は、はっきり言って、未解決です。 3つ目は地球磁気圏の後ろ半分に存在する、極域から出た磁場が後ろに引きずられた部分の話です。地球磁気圏の後ろ半分で、更にマグネトシースのすぐ内側にある磁場は、一方では地球の極域とくっ付いていますが、もう一方は太陽風に流されてずーっと後ろのほうまで引きずられています。これは見た目、マントを覆っているようなので、プラズママントル[plasma mantle]と呼ばれています。プラズママントルでは、希薄なプラズマが、外部のプラズマシースの流れに沿って、高速に流れています。 以上が磁気圏境界層の話でした。名前がゴチャゴチャして、分かり難いでしょうが、大事なことは、太陽風磁場と地球磁場が接する場所によって、そこに存在するプラズマの環境が異なるって事です。
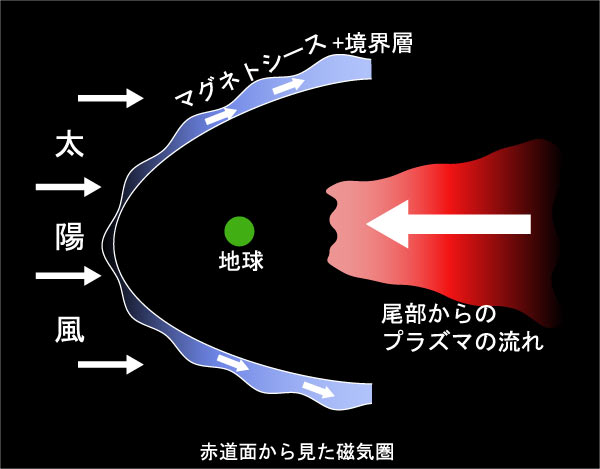
注釈:真北から地球磁気圏をみたら、こうなります。磁気圏境界層は、前面で薄く、横腹~尾部にかけて厚くなっています。境界層の中のプラズマ流は、外側のマグネトシースのプラズマ流によって尾部に向かいます。一方、磁気圏内部では、尾部から地球方向に流れるプラズマがあります。これは、遠くの尾部でプラズマ流の折り返しがあるためです。つまり、磁気圏では、プラズマは対流を起こしています。
では、話を地球磁気圏内部に移しましょう。 先程のプラズママントルは、後ろに行けば行くほどその厚みを増していきます。その結果、40万kmほど後ろで(この距離は大体、つきの軌道付近です)地球磁気圏の北半球と南半球に出来ていたプラズママントルが赤道面付近まで接近してきます。こうなると、赤道付近では高く加熱されたプラズマ領域が赤道面付近に形成されます。これをプラズマシート[plasma sheet]と言います。プラズマシートの厚さは数千km~数万kmといわれています。 プラズマシート内のプラズマはマグネトシースのそれと比べて、かなり加熱されて、希薄になっています。数字で表わすと、マグネトシースのプラズマがで10万℃、密度が30~50個/ccであるのに対し、プラズマシートでは温度が数百万℃、密度が1個/ccと言った具合です。 さて、いままでは太陽風、マグネトシース、地球磁気圏、プラズマシートの話でしたが、大事なところが抜けています。地球の近傍の話です。地球近傍は地球磁気圏の深部になりますが、地球磁場を出しているという意味では、磁気圏の出発点ともいえます。ではお話を再開しましょう。

注釈:地球近傍では双極子磁場(棒磁石の磁場)を作っています。この磁場は、磁気圏前面では圧縮され、逆に尾部では引き伸ばされています。磁場(この図の場合、磁力線と言ったほうが分かりやすいかも)はゴムひものような物で、圧縮されると押し返そうとし、引き伸ばされると引き戻そうとします。
地球の高度百数十kmに存在する、電離圏(若しくは電離層)[ionosphere]より高度の領域はプラズマ圏[plasmasphere]と呼ばれています。プラズマ圏の終端部分、つまりプラズマ圏界面[plasmapause]はおおよそ高度25600km~38000kmに位置します。プラズマ圏のプラズマは、比較的高密度で、低温(といっても通常よりうんと高いのですが)です。密度はだいたい100個/cc~10000個/ccで、温度は数千℃ です。

注釈:地球の上空には、気体分子、特に酸素や水素、窒素などが太陽光の紫外線を浴びて電離します。このとき、電離気体はプラズマとして振舞います。この写真は電離層の中にある、プラズマの密度分布を表わしています。特に高緯度地方に密度の高い領域があります。
さて、これで話は終わりですが、皆さん地球磁気圏が一体どう言うものか大体分かったでしょうか?地球磁気圏は僕らの住んでいる地上とはまるで様子が異なるのです。一つ例を挙げると、室温27℃の中で1ccの空気の中には、なんと空気分子が1億の1億倍の1000倍個もあるんです!それに比べたら地球磁気圏なんて滅茶苦茶希薄で何もないような気がします。でも、そんな希薄な世界から僕らは、時に美しいオーロラを授かり、時に世界的な電波障害(これは電離層と地球磁気圏がつながっている証拠)を被るのです。 今回紹介したプラズマは、光と同様、太陽から地球に届く媒体です。そしてそのプラズマを地球を結びつける物が磁場(磁力線)です。でも、プラズマも磁場も、地球以外の惑星、また他の恒星、銀河などにも観測されています。そうです、プラズマは宇宙全体を満たしているのです!ですので、地球磁気圏で起きていることをもっと詳しく調べたら、それはやがて、もっと広い世界への知識へとつながっていくのです。 どうです?夢のある仕事と思いませんか??
1.プラズマ粒子の運動って?
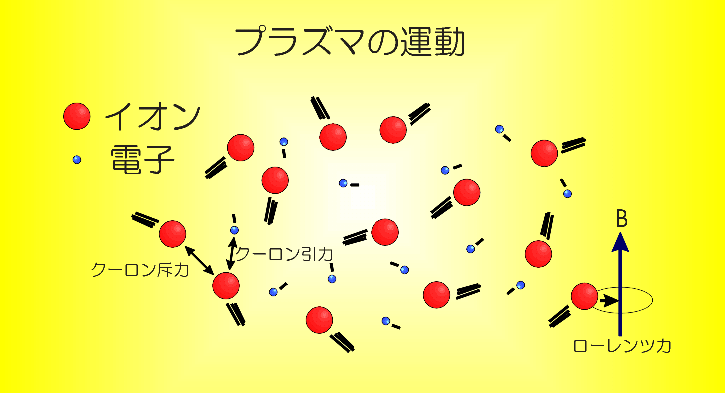
プラズマは、正電荷を帯びたイオン、負電荷を帯びた電子からなっています。宇宙空間では、ほぼ90%が水素で占められている、といわれますが、これは水素原子が電離し、陽子と電子にわかれた状態で存在しています。したがって、宇宙空間におけるプラズマ構成粒子は、そのほとんどが陽子と電子である、といえます。 プラズマを構成している粒子は電荷を帯びていますから、当然電磁場から力を受けて運動することになります。宇宙空間には、例えば地球磁気圏内であれば地球の固有磁場、また、地球磁気圏外では太陽起源の惑星間空間磁場などが存在しており、プラズマの運動はこういった磁場の存在に支配されています。そこで、粒子が磁場から受けるローレンツ力に注目してみましょう。ローレンツ力は、磁場の方向と粒子の速度に垂直な方向に力を及ぼします。ですから、粒子にしてみれば、ローレンツ力が向心力となり、磁場(磁力線)の周りをぐるぐると回るように運動します。このことをラーマー運動(もしくはサイクロトロン運動)、旋回半径をラーマー半径と呼びます。つまり、プラズマ粒子は磁場に縛られながら運動している、ということができるでしょう。 また、電荷をもった粒子が運動すれば、電流が発生します。電流が流れればそれにともない磁場が発生します(電磁誘導の法則)。これは宇宙空間に存在するプラズマと磁場にもいえることです。つまり、プラズマが運動することによって電流が流れ、それに誘導された磁場が発生し、外部から与えられた磁場をかき乱す。かき乱された磁場によってプラズマの運動は変化し、流れる電流も変化する。更に磁場を乱し・・・、というサイクルが成り立ち、系が全体として発展していくわけです。このようにプラズマの運動は非常に複雑なものになります。
2.電磁流体という考え方
1個1個の粒子すべての運動を追いかけて系全体としての発展を考えることができれば、それはもっとも素晴らしいことでしょう。しかし、それは非常に大変なことであり、複雑になり過ぎる、と考えられます。そこで、粒子の動きをある程度平均化して、流体として取り扱う(流体近似)、という考え方が生まれました。この考え方こそ電磁流体力学(MagnetoHydroDynamics: MHD)です。これは、簡単にいえば通常の流体力学における運動方程式にローレンツ力を加えたものであり、プラズマの運動はこの運動方程式によって記述されます。また、電磁場の発展はマックスウェル方程式に支配されます。 電磁流体力学では、「粒子の運動を平均化する」わけですから、個々の粒子の運動は表舞台から消え去ってしまいます。先ほど、プラズマ粒子は磁場の周りをぐるぐる回る、といいましたが、プラズマを流体として取り扱ってしまえばこの効果は無視されてしまいます。このぐるぐる回る運動だけでなく、粒子の熱運動などの効果もないものとなるわけです。というわけで、電磁流体力学の考え方に従えば、プラズマの運動をだいぶシンプルに追いかけていけそうだ、ということがわかります。プラズマ物理学では、この電磁流体力学に基づいてさまざまな電磁気現象を理解しようと努める人達がたくさんいます。
3.プラズマを流体近似すると、イオンと電子はどうなっちゃうの?
プラズマは正電荷をもつイオンと負電荷をもつ電子から成るといいました。それでは流体近似を課した場合、イオンと電子はどうなってしまうのでしょうか。 流体近似する際にその近似の程度によって次の3段階に分類されます。 * イオンと電子をそれぞれ別の流体として扱う、電磁2流体近似 * イオンと電子は別の流体として扱うけれども、電子の質量を0として扱うHall-MHD近似 * イオンと電子は全く同じ動きをするという(ある意味とんでもない)近似を課す単一流体MHD近似 これらはそれぞれどのような場合に用いられるのでしょうか。まず、単一流体MHD近似を考えてみます。 単一流体近似では、イオンも電子も全く同じように動く、と仮定しています。これはどういうことでしょうか。あまり良くない例えですが、まわりに存在する空気中には、窒素、酸素、二酸化炭素といった分子が含まれていますね。しかし、われわれはこれらをいっしょくたにして”空気”と呼び、一つの流体力学方程式をもちいて”空気”の運動を追いかけたりしています。本来、それぞれ分子量が違うのだから違う動きをしているはずですよね。なぜそれでいいのか。それは私たちが生活している空間のスケール(数メートルくらいでしょうか)に比べれば、分子量の違いからくる運動の差など問題にならないくらい小さいからです。ですから空気は空気として一つの流体として取り扱えるわけです。 イオンや電子はもっと小さいじゃないか、すぐに同じ運動をすると考えてもいいんじゃないの、と思うかも知れません。しかし、磁場があるんです!プラズマ粒子は磁力線のまわりをぐるぐる回る運動をします。この旋回運動の半径は数百キロメートル程度だといわれています。したがって、この運動が見えなくなるくらい、もっといえばすごーく軽い電子とイオンの運動の差がないと思っていいほどのスケールは…、となると、ものすごく大きなスケール(地球半径=6,400 キロの数倍~数十倍)になってしまいます。つまり、単一流体近似は、このような非常に大きな現象をつかまえるときには電子もイオンもおなじように動くとしていいでしょ、と主張しているわけです。 それではHall-MHD、電磁2流体近似はどのくらいのスケールを考えるのか、ということについては、次で説明したいと思います。
ここまでで、プラズマを考えるには、電磁流体近似を利用して考えるのが有効で、さらにその流体近似には段階があることを示してきました。では、様々な段階の流体近似はどのような場合に用いるのが適切なのでしょうか?
我々の研究室では、主に、数値シミュレーションを用いて宇宙空間のプラズマの動きを再現して、プラズマについて理解していこうという姿勢をとっています。しかし、シミュレーションするには計算機が解く方程式を計算機に与えてあげないといけません。その方程式として、1番分かりやすいのが、プラズマを構成する粒子の1個1個全ての運動方程式を計算してあげる「粒子計算」と呼ばれているものです。しかし、地球近くの宇宙空間で考えると、一般に宇宙は真空と誤解されているくらい密度が小さいとはいえ、1辺が100mの立方体の中に100億個程の粒子が存在することになります。我々が考えたいのは10000kmなどの大きなスケールの現象が主なのでこれら全部の粒子について1個1個の運動方程式を解くのは非常に難しいです。そこで流体近似をした方程式を計算機に与えることにします。
流体近似には、大きく分けて ①イオンと電子が同じ動きをするとした単一流体MHD近似(MHD) ②イオンと電子を分けて考えるが電子の質量を0と近似(Hall-MHD) ③さらに電子の質量も考慮した近時(2流体近似) の3種類の近似があります。直感的に分かるかもしれませんが近似レベルを小さくするほど計算機で解くのが大変(計算コストが大きい)になっていきます。つまり①が一番計算コストがかからないと言えます。
では、計算機の能力が高ければ①は使わなくなるのでしょうか?
それは、「no」です。各方程式にはそれぞれの役割というものがあり、それを使うのが適切な条件というものがあるのです。それが「スケール」に関する考え方です。 例えば電子とイオンのそれぞれの運動が無視できるくらい大きなスケールの現象を考える場合、電子を考えた②や③を用いても計算コストが無駄にかかるということになってしまいます。また、逆に電子を考える必要がある小さなスケールでの現象を考えるのに①を使ってしまっては電子の効果を考えることはできません。 このように、各方程式系にはそれぞれが適している「スケール」というものがあり、対象としている現象を考える時には、「スケール」の概念を持って、計算機に与える方程式を慎重に選ばないといけないのです。 電子の効果が無視できる「スケール」には①を、電子の効果を考える必要があるものの電子質量が無視できる「スケール」には②を、電子の質量も考えないといけない「スケール」には③を用いて計算する必要があります。
ここで、その1例をあげておきます。 これは「KHの渦」と呼ばれる宇宙空間にできるプラズマの渦についてのシミュレーション結果です。 左が①及び②の方程式で計算したシミュレーション結果で、真ん中が③の結果です。 ちなみに図は密度を表していて色が赤に近いほうが密度が大きいということになります。 1番右の図は真ん中の図について別の見方をした図です。(レントゲン写真みたいなもの。)
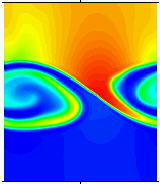
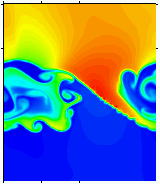
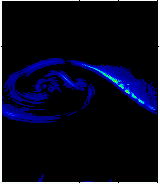
この渦の大きさは20000km程度の大きさです。つまり渦の大きさからすると電子の効果は無視できる「スケール」なので従来は① の方程式系で考えるのが妥当だと思われていました。しかし、渦の中心部分に注目して下さい。この部分では、密度の大きい部分(赤い部分)と密度の小さい部分(青い部分)の境目の長さが200km程度になっています。この長さというのは電子の質量を考えるべき長さなのです。ですので、従来とは違い③の方程式でシミュレーションしてみた結果①や②とは大きく違う結果が得られました。具体的には、境目が細くなっていた部分で特定の波長を持った不安定(電子の質量が原因)が発生していて(レントゲン写真に写っている。)この影響で①や②とは大きく違う結果になっているのです。しかもこの結果は今までの謎を解決するかもしれないものでした。
この例のように、「スケール」に関して考えるのは非常に重要であると同時に大切なことなのです。今まで①で十分だと思われていたものでも、局所的に電子の効果を考える必要のある部分が生まれたりすることも考えられるし、無視できると思われていた電子によるわずかな効果が結果的に大きな影響を与えることだってあるかもしれないのです。 しかし、前にも書いたようになんでもかんでも①を使わないで考えればいいという問題ではありません。②や③の方程式で計算すると電子によるいろいろな効果のために結果は複雑になります。上の例のように電子による効果が直接的に重要だった場合はいいのですが、ある現象を考えるときにその複雑さが重要ではない場合もあるのでその場合は、かえって②や③で計算してしまったことがマイナスになってしまいます。このように、「どの方程式を用いるか」を慎重に考え、これらの方程式をうまく使いこなすことが重要であり、難しさであり、面白さでもあるのです。
では、流体近似以外を用いるのはどのような場合?
今までは流体近似について考えてきました。しかし、現在計算機の能力は指数関数上に発展しているといわれており、流体近似を考えない「粒子計算」も徐々に行われてきています。
前にも書いたように流体近似には段階があります。そして、その流体近似の次の段階が粒子計算だと考えてください。より小さな「スケール」の現象を考えていくと①→②→③となりついには流体近似の次の粒子計算の範囲になるのです。
粒子計算にも段階があり、
④電子は流体近似のままで考えイオンのみ粒子化した方程式(ハイブリッド・シミュレーション)
④-1 電子の質量を0と近似
④-2 電子の質量を考える
⑤電子もイオンも粒子として考えた方程式(フル・パーティクル)
粒子という考え方をすると、流体近似のときにはなかった粒子が磁場にクルクルと巻き付く効果などがでてきます。これは「スケール」の小さな範囲の現象で す。しかし、電子の質量による効果もなかなか小さいものなので④-1と③はどちらが近似レベルの小さい現象かというのは微妙なところです。
これらを含めて近似レベル、すなわちその方程式系の解剖できる「スケール」の順としては
① → ② → ③ →④-2 → ⑤
④-1
ということになります。⑤がもっとも小さな「スケール」までを計算できる方程式だということになります。
しかし、いくら計算機の能力があがっても⑤で計算すれば全てを解明できるのではなく、小さい「スケール」まで考えればそれだけ現象が複雑になって、結果を 見ても何が起こっているのかよく分からなくなってしまうので、段階を踏んで徐々に近似レベルを小さくして一歩一歩現象を解明していくことも大切ですし、
「ここでは電子の効果が効いてくるはずだ」とか「ここでは粒子効果を考える必要がありそうだ」などと、その時に必要な方程式を見極めることも大切です。
従来は世間では何も考えず①を用いることが主だったので、本研究室では、このようないろいろな方程式系に注目して「方程式系を使いこなして」いろいろな現象を解明していこうとしています。
<Kenny>