最新研究成果

磁気圏わき腹境界層におけるプラズマの流れパターンの再現

長谷川　洋　／　助手

　Geotailなどの磁気圏・宇宙空間観測衛星は、衛星が飛んでいるその場所でのプラズマや電磁場について、三次元の速度分布関数や高時間分解波形など、精密な情報をもたらしてくれる。しかし観測データがどのような前後関係（衛星周辺の全体構造や大規模現象）の中で得られたのか良く分からないことが多いため、その解釈はしばしば困難をともなう。その場観測衛星が取得したデータから宇宙空間磁場の二次元像を再現する手法、グラッド・シャフラノフ再現法（以下、GS法）は、こうした中、10年ほど前に開発された。GS法では、衛星が軌道に沿って取得したプラズマ・磁場観測を初期値として用いて磁気ベクトルポテンシャルについてのGS方程式を解くことにより、磁力線の二次元平面への投影図を作成する（Hau & Sonnerup, 1999）。

　磁場構造の二次元像が得られるため、GS法は磁気圏界面の電流層や、コロナ質量放出（CME）にともなう太陽風中の磁気雲などの研究に大いに役立っている。しかし従来のGS法は、ほぼ静的平衡状態にある“磁力線”構造にのみ、適用が限られている。今回、プラズマ速度場つまり“流線”の二次元マップを再現するための新しいGS法を開発し、適当な条件下ではかなり正しい速度場を生成できることが分かった。また、Geotail衛星が磁気圏わき腹の境界層にいた時の観測データに適用し、結果に基づいて手法の可能性と限界について考察した（Hasegawa et al., 2007）ので、そのいくつかを紹介する。

　GS法は電磁流体力学（MHD）の理論に基づいているが、新手法が前提とするさらなる条件は以下の通りである：（１）構造が平衡状態にある（＝ある系で見た時に時間変化がない）、（２）構造は二次元である（＝ある方向ｚ軸沿いの空間勾配はない）、（３）磁場はｚ軸成分のみをもつ。このような仮定の下で、MHDの運動方程式を変形すると最終的に、

　　　　　　　　（１）

が得られる（Sonnerup et al., 2006）。ここでρはプラズマ密度、Ψは流線関数である（右辺RHSは幾つかの項を含む）。（１）式は、プラズマが曲がった流線に沿って動く時に働く遠心力と、全圧（プラズマ圧＋磁場圧）の勾配から生ずる力とがつりあっていることを表す。

　（１）式はGS方程式やポアソン方程式と似た形をしており、楕円型の方程式である。このタイプの方程式は普通、境界値問題として数値的に解かれるが、衛星観測の場合には軌道に沿って観測値が与えられるだけで、解きたい領域の境界全体に値が得られるわけではない。したがってGS法では、初期値問題として（１）式を解く。この際、衛星が観測した物理量の変動は空間構造によるものとみなす。最終的には、Ψのｘ−ｙ面での二次元分布が得られることになるが、流線はΨの等高線として表わされることになる。

　開発した数値コードは、流れ関数についてのGS方程式（１）の厳密解を入力することにより、期待どおりの性能を発揮することが確認できた。しかし現実の宇宙空間では、上記の3つの仮定のどれか（あるいはすべて）が破れることもあり、手法をさらにテストする必要があった。ここでは、その一手段として、ケルビン・ヘルムホルツ不安定の二次元MHDシミュレーションを用いた結果を紹介する。

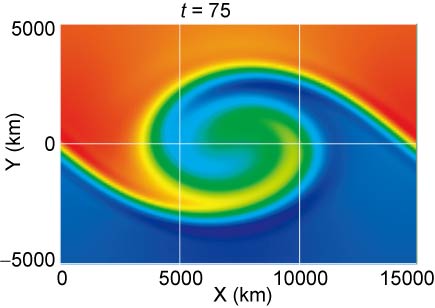
図１．ケルビン・ヘルムホルツ不安定の二次元MHDシミュレーション。色は75規格化時間でのプラズマ密度パターンを示す（赤：高密度、青：低密度）。

　図１はある計算時間でのプラズマ密度パターンを示している。初期条件としては、磁気圏わき腹で期待される平均的なパラメータを用いた（ｘ方向には周期境界条件を課している）。初期のプラズマは上半面で左向き、下半面で右向きの速度をもっていたが、図１の時間には不安定が成長して渦が巻き上がっていることが分かる。この瞬間にｘ軸に沿って得られるシミュレーションデータを、GS法の入力値として用いた。注目すべき点は、この擬似データは（１）式が意味する力のバランスを満たしていないということである（不安定はまだ成長途中にあり、平衡状態に達していないため）。図２はこうしてシミュレーションデータから生成された流線パターンである。渦構造がみごとに再現できているとともに、流線は真の速度ベクトル（シミュレーション結果）とほぼ平行であることが分かる。この結果から、現実に予想される程度の時間変化があっても、もっともらしい流線像が得られることが明らかになった。

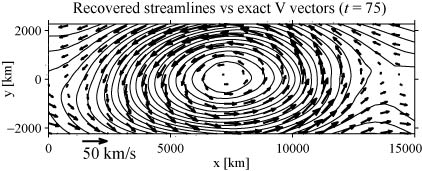
図２．図１のｘ軸上のシミュレーションデータから再現した流線パターン。実線は再現された流線、矢印はシミュレーション結果に基づいた正しい速度ベクトルを示す。両者は互いにほぼ平行であることが分かる。

　図３は、磁気圏夕方側のわき腹境界層で得られたGeotail観測データにGS法を適用した結果である。長さ２，３Re、幅１Re程度の渦が境界層に沿っていくつも並んでいたことが推察される。図中で衛星はｘ軸に沿って右に動くので、衛星が静止した系（磁気圏がほぼ静止した系）では、渦は左つまり反太陽方向に動いていたことになる。このような流線マップからは、衛星がどのような構造の中にいたのか分かるだけではなく、プラズマの輸送経路や輸送量に関する示唆も得られる。境界層ではプラズマ流によって磁場は変形されやすいため、先の（３）の（磁力線はまっすぐという）仮定が破れやすいことが予想される。今後、そのような状況にも対応できるよう手法を改善していく必要はあるが、今回開発したGS法は、磁場の効果を除いてやれば、中性流体にも適用できるものであり、宇宙プラズマ以外にも応用の可能性があるかもしれない。

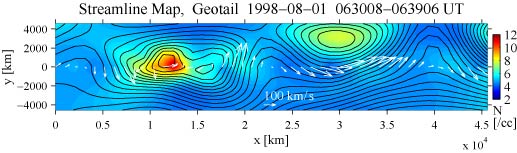
図３．Geotail衛星による夕方側の磁気圏境界層の観測から再現された渦の構造。色はプラズマ密度、白い矢印は実際に観測されたプラズマ速度ベクトルを示す。上側がシース、下側が磁気圏である。

 

参考文献

○　Hasegawa, H., B. U. O. Sonnerup, M. Fujimoto, Y. Saito, and T. Mukai, Recovery of streamlines in the flank low-latitude boundary layer, J. Geophys. Res., 112, A04213, 10.1029/2006JA012101, 2007.

○　Hau, L.-N., and B. U. O. Sonnerup, Two-dimensional coherent structures in the magnetopause: Recovery of static equilibria from single-spacecraft data, J. Geophys. Res., 104, 6899-6917, 1999.

○　Sonnerup, B. U. O., H. Hasegawa, W.-L. Teh, and L.-N. Hau, Grad-Shafranov reconstruction: an overview, J. Geophys. Res., 111, A09204, doi:10.1029/2006JA011717, 2006.