最新研究成果

電子温度非等方性は磁気リコネクショントリガーの救世主になるか？
田中　健太郎　／　研究員

 

■ イントロダクション

私たち宇宙プラズマを研究する者にとって，一つの大きな関心事があります．それは，プラズマ空間に蓄えられている電磁場エネルギーがどのようにプラズマ粒子のエネルギーに転換されるか？という疑問です．たとえば，太陽表面で発生するコロナ爆発現象では，高速に加速された（高エネルギーな）プラズマ粒子が太陽表面から吹き出しています．一方，地球上空で見られるオーロラ爆発現象では，高速に加速された（高エネルギーな）プラズマ粒子が地球上空に向かって降り注いでいます．これらの事実は既に過去の観測から示されているのですが，問題は，このような高エネルギープラズマ粒子がどうやって生みだされるか，と言うことです．

 

実はプラズマ粒子は，プラズマ粒子の存在する周辺の電磁場エネルギーを使って，自らのエネルギーを増大させることが出来ます．その実行手段として磁力線再結合過程（以下，磁気リコネクション）が長い間，考えら得てきました．今回の記事でもメインターゲットは磁気リコネクションです．

 

此処では，地球磁気圏尾部領域での磁気リコネクションに話を絞ります．地球磁気圏尾部領域では，図1 (a) にある様に，プラズマ粒子が濃い領域（電流層）を挟む形で強い磁場の領域 (ローブ領域) が両サイドから電流層を支えています．この状態から，もし図1 (b) の状態に電流層構造が変化したら，つまり，磁気リコネクションが発生したらどうなるでしょうか？電流層を構成するプラズマ粒子は，磁力線がゴム紐のような役割をし，プラズマ粒子をドーンッと加速させます．

 

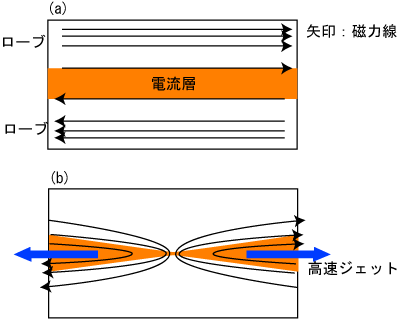
図1: 地球磁気圏尾部を模した，電流層の配置．(a) 初期状態．(b) リコネクション発生後の電流層構造とプラズマジェット．

 

 

では，図1 (a) から図1 (b) への状態に移り変わる事は，果たしていつでも起こりうるのでしょうか？答えはNOです．2次元粒子計算 [Tanaka et al., 2004] によると，図1 (a) の状態のまま，そっとしておいたときに（以下，「自発的」と言います），磁気リコネクションが発生するためには，電流層の厚さがかなり薄い，電子スケール程度（電子慣性長程度）に薄いことが必要とされます．一方で，電流層の長さを長くすると，さらに分厚い電流層であってもリコネクション活動を活発にすることが出来ることが，先行研究によって分かっています．ここで，Tanaka et al. [2004] の結果から必要な情報を取り出すと，電流層を長くした場合，活発な磁気リコネクションが起きるギリギリの電流層厚さは，0.5倍のイオン慣性長です．ただし，ここではイオン・電子質量比を400とします．

 

ここで注意しなければならないのは，Tanaka et al. [2004] の結果では，磁気リコネクションを活性化するためには典型的なイオンのラーマー時間に比べて，かなり長い時間を要してしまいます．実際の磁気圏尾部での観測 [Sergeev et al., 1990] によると，磁気リコネクションの活性化に要する時間は，もっと短いことが知られています．従って，どうやら地球磁気圏尾部領域でのプラズマ宇宙では，なにか他の，もう一ひねりしたからくりがあるんじゃなかろうか？？という自然な問いがここ最近出てきました．

 

実際には，ローブ領域がフンッと電流層を押しつぶしてドーンッとリコネクションが開始するなんてことが，ひょっとしたら本当なのかも知れないし，そう言うことが起こりうる (だろう) と思っていて，じゃぁ何が爆発的な磁気リコネクションを引き起こすのかって事が，面白いことであり，悩ましいことであり，知りたいことな訳で．．

 

■ シミュレーションの設計
　そう言う気持ちが有るのだけど，まずは千里の道も一歩から．いきなりフンッてローブを押すところから始める前に，電流層そのものがフンッと押された状態 [Chen and Palmadesso, 1984] を考えましょう．僕らの使っているツールは，電子ーイオンプラズマを両方とも粒子として取り扱う，粒子シミュレーション．その性質上，フンッと押すこと，つまりは圧力を加える事は，ある一方向の温度を上げることに対応する．

 

そんな状態って，どんな状態よ？と思う人もチラホラ．温度に方向？確かによく分からないですね．．だって，そんな状態に僕らは実感として，慣れてないから．そう，そこに常識や慣例では見えてこない，宇宙プラズマの旨みが有るんです．説明は敢えて省くとして (興味が有れば電話かメールでどうぞ) ，温度 (または圧力) に非等方性 (向きによって温度が異なる事) を与える事によって，電流層をフンッと押しつぶすことが出来るはずです．ここでは，まずは電子温度非等方性 [Karimabadi et al., 2004] について，幾つか調査してみましょう．

 

ここまでがこの新着論文を書くに至ったメインコンセプトです．なにが大事かというと，チョコっとだけ電流層の中にカラクリを与えたって感じです．要するに，そっと磁気リコネクションを起こすことから，ちょっと磁気リコネクションをいじると何がどう変わるか，それがどんな面白さを見せてくれるか？それを調べました．

 

図2を見てください．これが今回のコンセプトである，ブチッと電流層を押す，と言うことです．細かい設定を言い始めるとアレなんで割愛しますが (正確には，図2にあるように，電流層に平行な圧力を下げたのです) ，うまいこと初期設定を調節すると，[電流層を貫く方向の圧力] > [電流層に沿った方向の圧力]を保ったまま，初期状態は静かに維持されます．ただ，この状態はまるで，ドミノ倒しの初期設定と同じで，一寸でもぐらつかせると，ドドドドーンとドミノが崩れるかのように，電流層がドドドドーンと押しつぶされて，リコネクションが爆発する (だろう) 設定です．

 

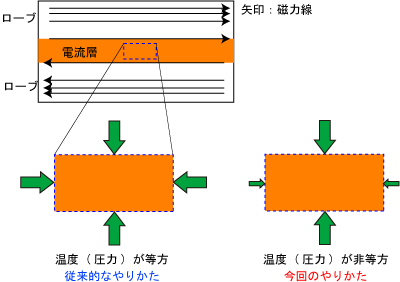
図2: シミュレーションの基本設計．今回は，電流層内部の温度を調節し，初期磁場方向の電子温度が磁場に垂直な電子温度よりも低くした．これによって，電子温度非等方性を実現した．

 

 

さて，このような予想がどこまで通用するのか，僕はパラメータサーベイを行いました．パラメータサーベイを行うに辺り，幾つか登場するパラメータを紹介します．まずはイオン・電子質量比．現実の値は大凡1836ですが，この値を使ってシミュレーションを行うことは現実的ではありません．というのも，イオン・電子質量比が増加すればするほど，計算機資源が爆発的に増加するからです．なので今回は，イオン・電子質量比 = 25, 100, そして400を用いました．次に，電流層厚さです．これは読んで字の如く，電流層の厚さ (ここでは半値幅) です．電流層の厚さは系統的に変化させました．最大で，イオン慣性長の2倍の分厚さの電流層を想定しました．最後に，電子温度非等方性です．電子温度非等方性 = [電流層を貫く方向の電子温度]÷[電流層に沿った方向の電子温度]で定義される量です．

 

■ シミュレーション結果

では，早速計算結果を見てみましょう．此処ではこの論文のハイライトを紹介します．図3は2つの異なる初期設定から始めたときの，電流層の2次元構造変化を時間に対して並べた物です．コンターの色は電子のプラズマ数密度，黒線は磁力線を表しています．

 

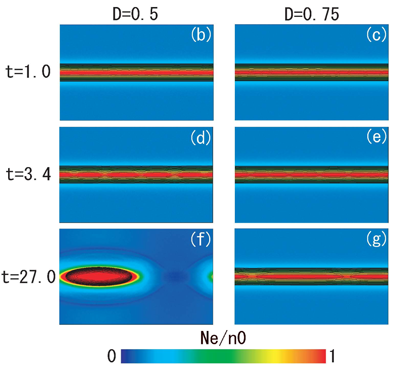
図3： 初期電子温度非等方性αeoをαeo = 2.0に固定した下で，初期電流層厚さDが与える，磁気リコネクション活動（ティアリング不安定性の成長）の変化．
D = 0.5 versus 0.75 at Lx = 24D, M = 400, αeo = 2.0
(b) t=1, (d) t=3.4, (f) t=27での，D= 0.5の時のプラズマ密度の2次元スナップショット．黒線はt=0における，|z|<Dの磁力線．t=1では，電流層中心にのみ電子温度非等方性ティアリング不安定性により，短波長モードの磁気島が観測される．t=3.4では，電流層中心での磁気島がさらに成長を継続させる．t=27では初期電流層を破り尽くす程度に成長した磁気島が形成される．

磁力線は初期の電流層の厚さ以内の物だけ表示させています．左半分のパネルは，初期設定が，イオン・電子質量比 = 400，電流層の厚さ = 0.5倍のイオン慣性長，電子温度非等方性 = 2です．右半分のパネルは，初期設定が，イオン・電子質量比 = 400，電流層の厚さ = 0．75倍のイオン慣性長，電子温度非等方性 = 2です．

計算開始直後（時刻 t = 1）では，両者の構造変化に何ら違いが見られません．そしてよく見ると，電流層の中心に非常に小さなポコポコの構造が現れています．このようなポコポコの構造のことを，磁力線によって囲まれた，「磁気島」と呼びます．ここではそのサイズの小ささから，「チビ磁気島」と名付けます．実は，このチビ磁気島，初期の電子温度非等方性の存在によって生じるものです．ここまでは厚さに依らず同じような磁気島の構造を見せるわけですが，さらに時間が経つと，電流層の厚さによって，二次元構造が変化します．次の時刻の図(t = 3.4)を見てください．赤色のコンター付近に注目すると，その付近での磁力線の厚さに違いが見られます．D = 0.5の方が，より太くチビ磁気島 (磁力線の輪っか) が太ってきています．さらに時間が経つと(t = 27.0)，D = 0.5の場合は完全に一つの大きな磁気島が形作られています．このとき，元々の電流層の厚さを超える磁気島の太さに成長していることが分かります．ところが一方，D = 0.75の場合ですと，磁気島は電流層中心付近 (赤色付近のこと) 程度の薄さしか成長していません．

此処で思い出して欲しいのは，自発的な磁気リコネクションの場合でも，D = 0.5の場合ではリコネクションが活性化し，D = 0.75の場合では磁気リコネクションが顕著でないことです．つまり，電子温度非等方性は，磁気リコネクションの成長速度を上げることは出来ても，活発な磁気リコネクションをより分厚い電流層にもたらすことが出来ないのです！

 

■ まとめ
　結局，電子温度非等方性のやったことと言えば，スタートダッシュの速さをうんと高めただけで，最終的なゴールのレベルそのものを高めることが出来なかったのです．．なので，当初期待していた，電子温度非等方性は磁気リコネクションを素早く，かつ爆発的に発達させるには至らなかったのです．

 

　ただ，電子温度非等方性の持つ，成長率の増加をうまく使えば，自発的な磁気リコネクションよりも素早く引き起こせる希望が生まれました．実は，最近の私たちの予備的計算結果によると，イオン温度非等方性と電子温度非等方性とのカップリングによって，二段階のリコネクション加速段階が発生することが分かりました．しかも，最終的なリコネクションの飽和レベルも十分に大きく発達しました．

 

　現在，電子温度非等方性・イオン温度非等方性のカップリングによる超素早い，爆発的磁気リコネクションに関する論文執筆に取りかかりました．みなさん，こうご期待！！

 

■ 参考文献
○ Haijima, K., K. G. Tanaka, M. Fujimoto, and I. Shinohara (2007), Electron temperature anisotropy effects on tearing mode in ion-scale curretn sheets, J. Adv. Space Res., in press, doi:10.1016/j.asr.2007.05.049.

○ Tanaka, K. G., I. Shinohara, and M. Fujimoto (2004), Critical thickness for two-dimensional tearing instability, Geophys. Res. Lett., 31, L03808, doi:10.1029/2003GL018955.

○ Chen, J. and P. Palmadesso. (1984), Tearing instability in an anisotropic neutral sheet, Phys. Fluids, 27, 5, 1198.

○ Karimabadi, H., W. Daughton, and K. B. Quest (2005), Antiparallel versus component merging at the magnetopause: Current bifurcation and intermittent reconnection, J. Geophys. Res., 110, A03213, doi:10.1029/2004JA010750.

○ Sergeev, V. A., P. Tanskanen, K. Mursula, A. Korth, and R. C. Elphic (1990), Current sheet thickness in the near-earth plasma sheet during substorm growth phase, J. Geophys. Res., 95, 3819.