最新研究成果
Cluster-II衛星が観測した衝撃波面再形成
関 克隆 / 博士課程
1.衝撃波は高エネルギー粒子の生成工場
太陽風プラズマはその密度が非常に希薄なため,構成する粒子間のクーロン衝突がほとんど無視できる無衝突プラズマである.無衝突プラズマ中では,粒子の分布関数はマクスウェル分布であるとは限らず,平均的な運動量を逸脱した非熱的粒子が生成されることがあり,衝撃波はそのような高エネルギー粒子の生成場所として考えられている.このことはSUZAKUによる最新の衝撃波研究により,さらなる確証を得た.「超新星爆発の衝撃波で宇宙線は極めて短時間(1年程度)で加速されていた」(http://www.isas.ac.jp/j/topics/topics/2007/1004.shtml)
このような状況のなかで,in-situ観測可能な地球定在衝撃波の研究は,天体での非熱的粒子の生成機構,高エネルギー宇宙線の研究にとっても重要なものとなっている.
2.本研究の特色 〜多点同時観測の重要性〜
本研究の目的は,その場観測データを用いて地球定在衝撃波(Bow shock)における非熱的粒子の生成プロセスを理解することにある.Bow shockを研究することの最大の利点は,直接その場にいって観測すること(in-situ 観測) が可能である点である.従来の地球Bow shockの観測的研究では,主に一衛星のみの観測であったために衝撃波面は局所的には空間的に一様であり時間変化していないと仮定し議論されていることが多かった.しかしながら,理論・数値シミュレーションを用いた研究により,衝撃波面は定常状態とは限らないことが報告されている.衝撃波面に沿って伝播する空間的変動はリップル構造として知られており,一方,衝撃波面のその場の時間的な変動は衝撃波再形成(リフォーメーション)として知られている.また,このような衝撃波面の非定常性が衝撃波遷移層でのエネルギー散逸に大きな影響を及ぼすことが示唆されている(Lembege et al., 1992, Scholer et al., 2003, Hoshino and Shimada, 2002, Lowe and Burgess, 2000).
しかし,これまでのような一衛星観測では,時間変化と空間変化を完全に分離することはできないので,衝撃波面の非定常性を示すことは非常に難しい.1衛星による観測データだけでは,得られた時系列データがその場の時間発展なのか,空間構造が伝播した結果を示しているのかわからない.過去にISEE1-2の2衛星を使用して非定常性の同定を試みた例もあるが,はっきりとした結論は得られていない.したがって、できるだけ多くの場所で同時観測し各衛星から得られたデータを合わせることで,その場の時間的発展なのか空間構造によるものなのかを理解することが不可欠である.三次元的空間構造をきちんと理解するには,最低4つの衛星が必要である.
3.編隊観測で初めて観測した衝撃面の非定常性
このような背景から,本研究では編隊観測をしているCluster-II衛星4機を用いて衝撃波面の非定常性,特に衝撃波面の時間変動であるリフォーメーションを同定することに焦点を絞り解析した.
Cluster-II衛星は,2000年にESA(欧州宇宙機関)により打ち上げられた4衛星による編隊観測衛星である.本研究に用いたデータは,Cluster-II衛星に搭載されている磁場観測装置(Fluxgate Magnetometer: FGM),電場観測装置(Electric Field and Waves: EFW)より得られた高時間分解能の電磁場データとイオン粒子観測器(CIS)で得られた4秒値のデータである.
図1は,2002年4月20日05:18(UT)にCluster衛星が上流から下流にかけてbow shockを観測した時の4秒間のデータである.各衛星から得られた衝撃波上流のパラメータの平均的な値は,ΘBn83-89 [deg],MA 3.1,β0.4(ΘBn:衝撃波面法線方向と上流磁場のなす角,MA:衝撃波上流のバルク速度とアルフベン速度との比,β:プラズマの圧力と磁場圧の比)である.この時の衛星間距離は110-180 [km]であり、非常に短い時間差で衝撃波を観測しているにも関わらず,磁場・電場データともに,衛星毎に異なった衝撃波構造を観測しており,衝撃波面が非定常であることがわかる.
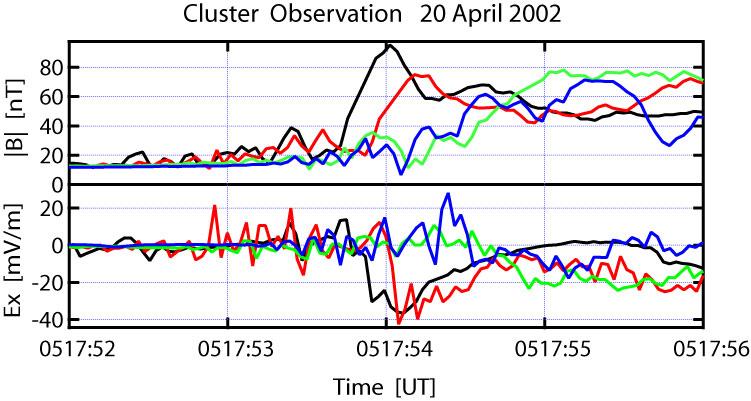
図1. 2002年4月20日05:18 UTにCluster衛星が地球bow shockを上流から下流にかけて観測した際の衝撃波遷移層4秒間のデータ.上のパネルはFGM (22 Hz sampling)で得られた磁場の絶対値,下のパネルはEFW(25 Hz sampling)で得られたGSE座標系(Geocentric Solar Ecliptic coordinate)でのx成分の電場データである.横軸は時間で,色は観測衛星を示しており,黒:Cluster1号機(s/c1),赤:s/c2,緑:s/c3,青:s/c4に対応している.
4.大規模数値計算と観測結果との比較
衝撃波面に沿った空間的変動であるリップル構造は,波長が1000~2000 [km],振動周期は〜16秒であるという観測結果がある(Moullard et al. 2006).この時の衛星間距離はリップル構造と比較してとても小さいので一次元的な構造の時間変化であると考えられる.そこで,観測されたパラメータをもとに一次元の粒子シミュレーションを行い,仮想衛星による観測を行った.その結果,観測と同様なパラメータでのシミュレーションにおいても衝撃波面のリフォーメーションが起こっていることが確認でき,また衝撃波遷移層において電子加速の原因となる波が励起されていた(Wu et al., 1984).この波は入射イオン・電子と衝撃波面で反射されたイオンとの間の相互作用によるものである。図2がそのシミュレーションの結果である.(a)(b)(c)(d)はある1リフォーメーション周期の異なる位相を示しており,(d)から(a)は衝撃波面が急峻化していく位相,(b)から(d)は入射粒子と反射粒子による不安定性によって波が励起され衝撃波面が崩壊していく位相を示している.(c)(d)においては,衝撃波遷移層において変形2流体不安定性(Modified Two Stream Instability :MTSI)による波が励起され電子が加速されている様子が確認できる.
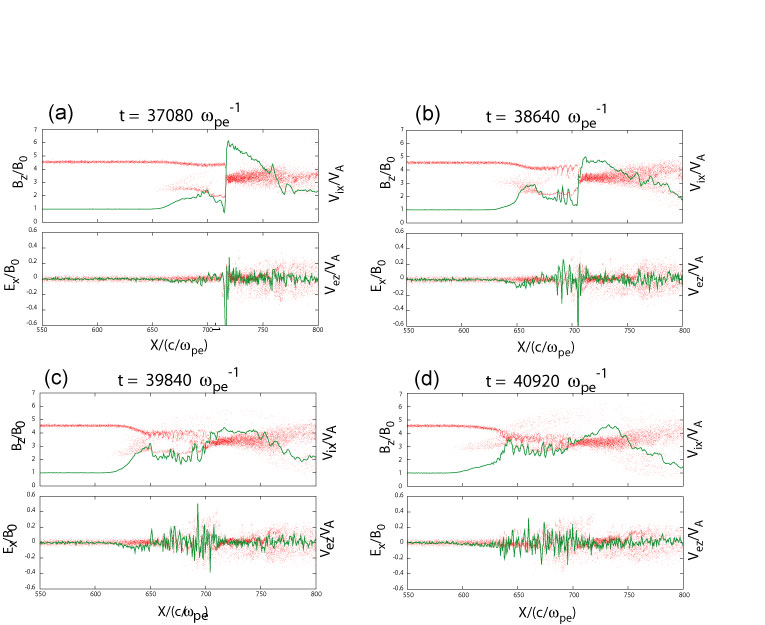
図2. 1次元粒子シミュレーションによる衝撃波面遷移層の構造と粒子分布.(a)(b)(c)(d)とも同じフォーマットで,上のパネルでは緑のラインが磁場強度,赤が速度空間でのイオンの分布を,下のパネルでは緑のラインが電場のX成分(衝撃波法線成分),赤が速度空間での電子の分布を示している.
図3は,実際にClusterが観測したデータと仮想衛星による観測結果を比較したものである.各仮想衛星は1リフォーメーション周期の異なる位相を観測しており,このシミュレーション結果は,Clusterの各衛星が観測した結果とよく一致しているのがわかる.SC1 (Cluster衛星1号機)【VS1 (仮想衛星1号機)】が衝撃波面の急峻化した位相を観測し,SC3(VS3)では衝撃波面が崩壊していく位相を観測していたことがわかる.さらに,シミュレーションで観測された波とSC3,SC4が衝撃波遷移層で観測した波の周波数・電場の振動方向とも一致していた.シミュレーションからは再現することができなかったが,SC2が観測した波はSC3・4と同様の波であると考えられる.
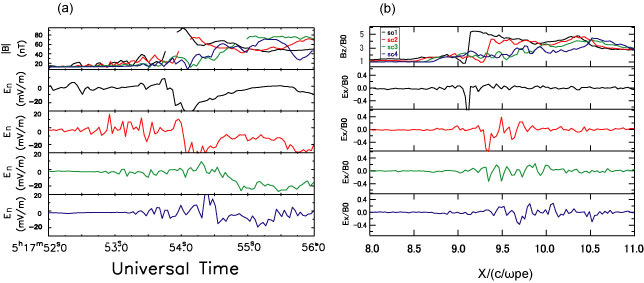
図3. (a)Cluster観測データ (b)1次元粒子シミュレーションによる仮想衛星観測データ.(a)(b)ともフォーマットは同じで,上から磁場の絶対値,SC1 (VS1),SC2 (VS2),SC3 (VS3),SC4 (VS4)が観測した電場の法線方向成分(SC:Cluster-IIの1-4号機,VS:仮想衛星1-4号機).
シミュレーションから予測されるリフォーメーション1周期は,1-2イオンジャイロ周期程度である.このイベントの観測データから推定したリフォーメーション周期は約2秒である.この時の衝撃波面法線方向の衛星間距離は80 [km]以下であり,1.5秒で4衛星が衝撃波を横切ったため,シミュレーション研究から示唆されていた垂直衝撃波面がリフォーメーションしていく様子を初めて直接観測することができた.
5.課題
次なる課題は,衝撃波面のリフォーミングに伴い電子がどのような振る舞いをしているのかを理解することである.現在,Cluster/PEACE電子観測器の1エネルギー掃印ごと(125 [ms])のデータを用いて,衝撃波遷移層での電子ダイナミクスに迫っている(参考:Geotal,Cluster時間分解能 (通常観測モード):12 [s],4 [s],電子の典型的な時間スケール <10 [ms]).
参考文献
1. B. Lembege and P. Savoini: Nonstationarity of a two-dimensional quasiperpendicular supercritical collisionless shock by self-reformation, Physics of Fluids B: Plasma Physics , Vol. 4, 3533-3548, (1992)
2. M. Scholer, I. Shinohara and S. Matsukiyo: Quasi-perpendicular shocks: Length scale of the cross-shock potential, shock reformation, and implication for shock surfing, J. Geophys. Res., Vol. 108, 1014 (2003)
3. M. Hoshino and N. Shimada: Nonthermal Electrons at High Mach Number Shocks: Electron Shock Surfing Acceleration, The Astrophysical Journal, Vol. 572,? 880?887, (2002)
4. R. E. Lowe and D. Burgess: Energetic electrons downstream of Earth's bow shock: Simulations of acceleration by shock structure, Geophys. Res. Lett, Vol.27, 3249-3252, (2000)
5. Moullard O., D. Burgess, T. S. Horbury, and E. A. Lucek, Ripples observed on the surface of the Earth’s quasi-perpendicular bow shock, J. Geophys. Res. Vol. 111, 9, A09113, (2007)
6. Wu, C.S., Winske, D., Zhou, Y.M., Tsai, S.T., Rodriguez, P., Tanaka, M., Papadopoulos, K., Akimoto, K., Lin, C.S., Leroy, M.M., Goodrich, C.C. Microinstabilities associated with a high Mach number, perpendicular bow shock, Space Sci. Rev. 63-109 (1984)