最新研究成果

その場観測からプラズマ構造の時間発展を再現する

長谷川　洋　／　助教

 

我々の分野のプラズマや電磁場の観測器は、衛星が飛んでいるその場所での情報しか得ることができず、宇宙空間で起きている現象の空間変化と時間変動を把握することは簡単ではありません。衛星は、非一様な構造が時間発展している中を、移動しながら観測しているからです。そうした状況では、時系列データが空間構造を反映しているのか、あるいは時間変動を反映しているのか、一点観測から判別することは困難です。そこで何らかの仮定と物理法則を用いてデータを解釈することになります。例えば、構造は平面的（一次元的）であるとか、定常状態にあるという仮定です。しかし実際に起きている宇宙プラズマ現象の多くは、多次元的かつダイナミックに変動しているので、なるべく解析手法の制約を小さくしてデータを解釈できるのが理想です。ここで紹介する新しいデータ解析手法の開発は、その理想に向けての一ステップです。

まず今回の手法では、プラズマ構造が二次元的で、ほぼ静的な平衡状態にあると仮定します。ここで静的とは、磁気張力と全圧の勾配力がほぼつりあっており、構造と共に動く系ではプラズマの流れ（慣性の力）は無視できるほど弱いということです。このような制約の下で、我々は磁場・プラズマ構造の時間発展を、その場観測のデータから再現できることを発見しました（Sonnerup & Hasegawa, 2010）。

図１．　時間発展再現法の概念図。

 

図１に開発した時間発展再現法の概念図を示します。衛星の軌道はX軸に相当し、この軸上に、ある時間帯の観測データを配置します。この時、観測データはある瞬間ΔT=0に得られたと仮定します。次に、この初期値を時間発展の方程式系を用いて時間軸方向に積分することにより、ΔT=0の前後の時間帯について、Y=0の面上でのプラズマや磁場の値を再現します。最後に、各時間ステップについて、Y=0上での再現値にグラッド・シャフラノフ（GS）法（Hau & Sonnerup, 1999）を適用することにより、ΔT=0の前後の時間帯について、磁場・プラズマ構造のXY面での二次元マップを得ます。GS法とは、その場観測の一次元情報から衛星軌道の周辺の磁場・プラズマ構造の二次元像を再構築する手法です。結果として、衛星観測の前後の時間帯についてのプラズマ構造のムービーができあがります。

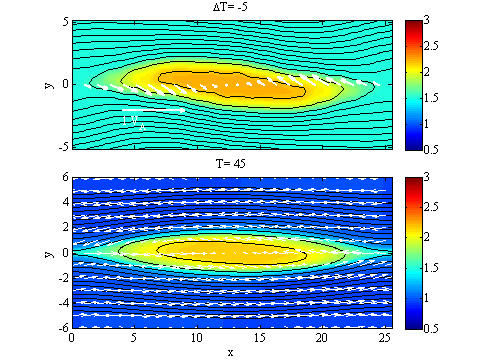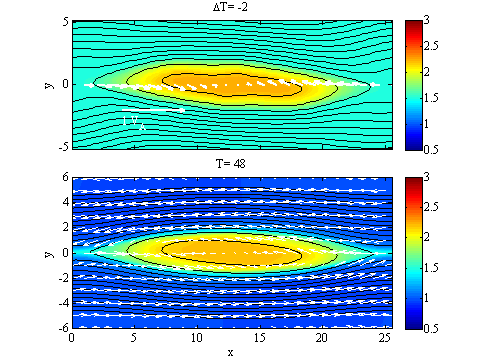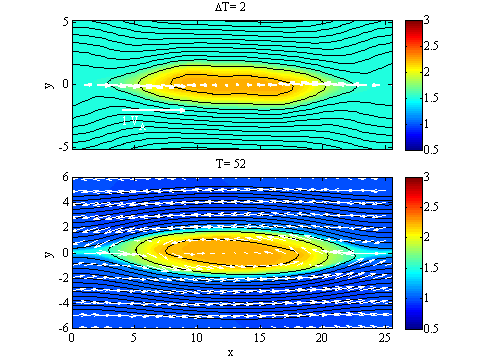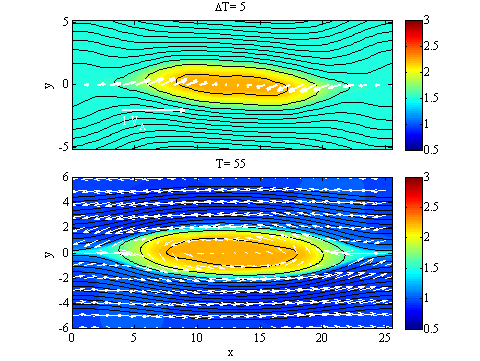
図２．　疑似観測データ（ある瞬間にX軸に沿って得られた一次元情報）から再現された磁気フラックスロープの時間発展（上）と、疑似観測に用いたシミュレーション結果（下）。黒線は磁力線を、色はプラズマ圧を示す。

 

図２に時間発展再現法のテスト結果を示します。下の図は、磁気リコネクションによって成長する磁気フラックスロープの二次元電磁流体シミュレーションの結果です。上の図は、シミュレーション時間T=50のX軸上での物理量（疑似観測による一次元データ）から再現された、磁場・プラズマ構造の時間発展を示しています。両者がよく一致しており、磁力線の運動がかなりよく再現できていることが分かります。

 

図３．　クラスター衛星が観測した磁気圏界面磁気フラックスロープ（図をクリックすると、時間発展ムービーが表示されます）。

 

図３は、時間発展再現法をクラスター衛星による実際の観測データに適用した結果です。この時、クラスターは磁気圏の昼側高緯度の境界付近で、磁気フラックスロープを観測していました。フラックスロープ中の磁力線はX軸方向に動いており、磁気リコネクションが進行していることや、フラックスロープがゆっくりと収縮していることが分かります。二次元構造という制約の下ですが、各々の磁力線の動きを追っていくことができるので、リコネクションの効率（つなぎかわる磁束の量）を推定することも可能です。

このような手法は、準静的なプラズマ構造だけでなく、プラズマ流の慣性力が重要になってくる場合にも拡張できる可能性があります。例えば、ここで紹介した手法とは異なりますが、電磁流体プラズマ構造の二次元像を衛星観測から再現する手法があります（Teh & Sonnerup, 2008）。この手法によって再現されたプラズマや電磁場の二次元場を、既存の二次元電磁流体シミュレーションの初期条件として用いることにより、実際に観測されたプラズマ構造の過去と未来を調べることができるかもしれません。

 

以上の結果は、Journal of Geophysical Research-Space Physicsに出版されました。

参考文献：

Hau, L.-N., and B. U. O. Sonnerup (1999), Two-dimensional coherent structures in the magnetopause: Recovery of static equilibria from single-spacecraft data, J. Geophys. Res., 104, 6899-6917.

Sonnerup, B. U. O., and H. Hasegawa (2010), On slowly evolving Grad-Shafranov equilibria, J. Geophys. Res., 115, A11218, doi:10.1029/2010JA015678.

Teh, W.-L., and B. U. O. Sonnerup (2008), First results from ideal 2-D MHD reconstruction: magnetopause reconnection event seen by Cluster, Ann. Geophys., 26, 2673-2684.